“The important lesson I wanted to show you here is that EIGRP uses the slowest bandwidth in the path and the sum of delays” I don’t understand. Wasn’t it supposed to be the sum of the metric of the path links???
I mean…if R5 is announcing a route, (assuming lowest metric is through R2) the feseable distance from the point of view of R1 would not be the sum of the metric of the links R1-R2-R3-R5 + the metric announced by R5 for that given route?? I am pretty sure it is… but the result is not the same as depicted here so I am a bit confused.
As always very thanks in advance!!!
Hello Jorge
EIGRP doesn’t work like OSPF where you simply sum the metric of each link along the path to get a total cost for a path. The metric is assigned and is actually defined on a per-path basis using this metric formula. Actually, what Rene is describing here is the way in which metric is measured, by definition.
In this particular part of the lesson, we are calculating the metric from R1 to R5 using the path R1-R2-R3-R5. When we do so, we use the EIGRP metric formula. What do we put in the “bandwidth” variable? There are so many different bandwidths in the links between these routers! By definition, however, we use the lowest bandwidth only, in other words, the link which causes the bottleneck. Remember, we’re not calculating the metric on each link, but the metric for the total path. That’s how EIGRP works.
However, when it comes to the delay component of the metric, we count the cumulative delays introduced by all links, so we must sum them. Once again, this is by definition how we calculate metric in EIGRP.
Not quite. When R5 announces a route to, say its loopbak interface, that information will be propagated to R3, R2, and R1, and along the way, EIGRP will learn the delays and the bandwidths of each link. Once R1 receives this info, it will calculate the metric to the destination by first using the metric formula as we described, and then adding to that the metric announced by R5 to the destination in question.
PS in this lesson, we can assume that the destination being advertised by R5 is the interface directly connected to R3, so there is no “additional metric” announced by R5. So we’re looking purely at the metric from R1 to that particular interface only.
I hope this has been helpful!
Laz
What will happen if my FD is bigger than the 32bit ??
How it scales with RIB and whats the ranges ??
Hello Narad
The maximum value that you can get with the classic EIGRP formula is 4,294,967,295. Using an online EIGRP metric calculator, I tried to find the combinations that would exceed that value. In order to do so you must set the delay to an extremely large number, and most IOS versions limit this number to somewhere around 16 million. You must also set the load very high, and you must take into account the other K values.
The highest value I was able to get (limited to 16 million for the delay) was around 5,549,000,000, which is indeed larger than a 32 bit value can represent. However, such a scenario is so rare that it doesn’t affect the operation of EIGRP. In such cases, EIGRP will use the highest value of 4,294,967,295 for the result of that formula.
Of course, EIGRP wide metrics is a new way of calculating EIGRP metrics that uses a 64-bit value. However, this was done to make the metrics more accurate for high bandwidth interfaces and was not necessarily done in order to achieve higher metric values. You can find out more about this in the following lesson:
I hope this has been helpful!
Laz
HI Rene,
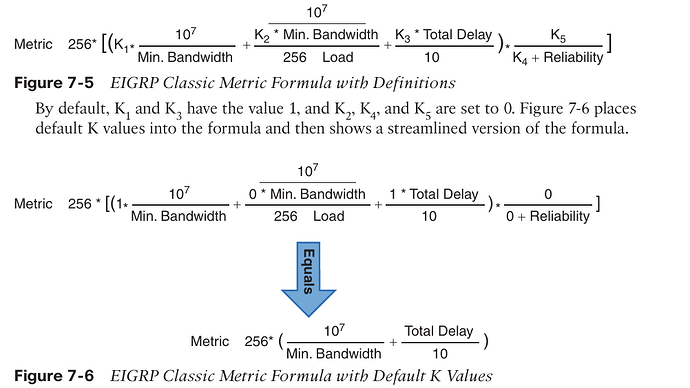
Could you explain a bit more the metric formula. In the OCG, the formula is presented as follows. Which does give different results.
Hello Artur
Rene uses the following in the lesson:
Metric = [K1*bandwidth + ((K2*bandwidth)/(256-load))+K3*delay]
In the above formula, it is assumed that K4 and K5 are zero, which is the default. He then says that if K4 and K5 are not equal to 0 then the formula becomes:
Metric = Metric *[K5/(reliability+K4)]
Where the second Metric that I’ve bolded represents the whole first equation above. So if you write it all out, it becomes:
Metric = [K1*bandwidth + ((K2*bandwidth)/(256-load))+K3*delay]*[K5/(reliability+K4)]
Now, later in the lesson, Rene clarifies what bandwidth is:
Bandwidth= [10^7 / minimum bandwidth in the path] * 256. In the formula you shared, that 256 multiplier is applied outside of the brackets.
So ultimately, the formula is the same, however Rene has written it out differently. I will let Rene know to see if he can clarify the way the formula is written in the lesson to be clearer.
I hope this has been helpful!
Laz
Hi Laz,
Thanks for the explanation. I was quite confused when I first tried to compare the two!
Thanks.
I am still not sure about the value 256 we use for the multiplication!!
Hello Speedosuper111
These NetworkLessons notes should clarify the purpose and use of the 256 multiplier. Take a look and if you have any other questions, let us know!
I hope this has been helpful!
Laz
Hello Laz,
Question regarding the metrics that EIGRP uses that were described in the lesson.
I understand that EIGRP uses the K values mentioned in the lesson for its overall metric calculation, and that by default only K1 and K3 are enabled. Isnt the metric we are calculating just the feasible distance? We always say EIGRP can use bandwidth, delay, reliability, and load as different attributes that we can use to calculate the overall metric, but Isnt the overall metric just the FD?
I understand that the successor, which is the best path to a particular destination network from the point of view of a particular router, is chosen from which path in the EIGRP topology table has the lowest feasible distance to a particular destination network. Once the successor is installed on the routers RIB, that specific EIGRP route will show the feasible distance as its metric in the portion of the route that shows the AD/metric.
So isnt the metric that EIGRP uses just the feasible distance? In other words, do the formulas presented in this lesson with the various K values just equal the FD?
Thank You Laz
Hello Paul
Yes indeed, the feasible distance is the metric of a particular path. But let me clarify some definitions so we can be more specific.
The EIGRP formula calculates the metric to a particular destination over a specific path. Whether or not all parameters (delay, load, bandwidth etc) are used depends on the K values as you suggested. The result of the formula calculation is a 32-bit value between 0 and about 4.2 billion (assuming we’re not using wide metrics).
To understand the term feasible distance (FD) more specifically, let’s recap some other terminology.
- The successor is the best next-hop router to reach the destination. It is the way to send the packet via the best path based on the measured metrics
- The feasible successor is the backup path with the second-best metric, assuming the feasibility condition is met.
Now, in this context, the FD is the metric of the successor. So it’s not just metric in general, but specifically the metric of the best path from the point of view of the local router.
Similarly, advertised distance (AD) is also a metric, but it is the metric that is reported by a neighbor to reach a destination. So yes, FD is the metric, but a very specific metric from the point of view of the local router.
The formula used here is a general formula to measure metrics. Whether that’s the FD or the AD depends on the context and the point of view of which EIGRP router we’re looking at. Does that make sense?
I hope this has been helpful!
Laz