EIGRP Wide Metrics

Lessons Discussion
21

Hello Christopher

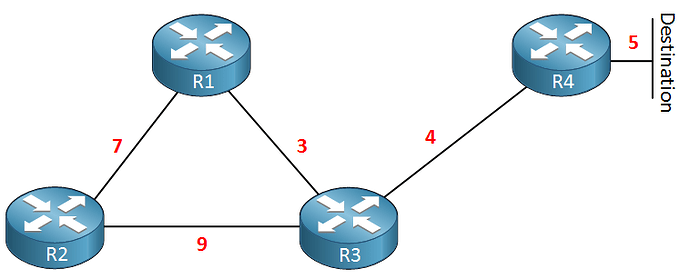
Unlike OSPF, EIGRP doesn’t provide a full picture of the whole network topology to each router. But the question remains, how does a particular EIGRP router “know” about the cost of the whole path to the destination if it doesn’t have this information? Well, take a look at this network topology with the EIGRP metrics noted for each link:

image
image758×307 31.2 KB

When R4 advertises the destination network to R3, it says “my distance to the Destination is 5”. That’s the advertised distance. When R3 receives that information, it will add a value of 4 to that metric, because it knows that the cost of its link to R4 is 4. So when R3 records the metric to the destination, it will say 5+4=9.

When R3 advertises that network and its metric to R2, it will say, “my distance to the Destination is 9”. R2 will receive that and it will add a value of 9 to that, which is the cost of the local link to R3. So when R2 records the metric to the destination via R3, it will say 9+9=18.

So you see, each EIGRP router will simply add to the advertised metric the cost of the link through which the path was learned, thus obtaining a cumulative cost to the destination, without the need to “know” the topology of the whole network. Does that make sense?

I hope this has been helpful!

Laz

22

Somewhat. I guess i have to presume that instead of R2 knowing that the AD(or BW) is is just simply 9, somehow it must be provided with the individual AD’s (or BW’s) along the path because it is a requirement for end to end K1 calculation. Maybe only the lowest bandwidth info is passed along.

Wish that part was spelled out somewh
ere.

23

Hello Christopher

Let’s take a deeper look into this one. Each EIGRP router when advertising a network, will use the EIGRP formula to determine that metric.

  1. So R4 has the destination as directly connected. Using the formula, and taking into account the bandwidth of the link, it measures a metric of 5. R4, in its update to R3, will send that metric which is the advertised distance.
  2. R4 will receive that information, and will rerun the EIGRP formula, and will take into account the characteristics of its link to R4. Based on the formula (including the bandwidth of the link), it generates a metric of 9 for itself to the destination. It shares that with R2.
  3. R2 receives the advertised distance of 9 from R3, and runs the EIGRP formula and takes into account the link between R2 and R3. The result is a metric of 18.

Now this is a simplistic description. In truth we’re not just summing costs, but we’re using the EIGRP formula to determine the cost. The outcome of the formula itself that R4 originally generates has embedded in it, the BW of the link to the destination. Similarly, R3, uses this advertised metric and recalculates the cost using the formula. R3 will take into account the bandwidth of the link to R4 in the metric it sends to R2. So R2, although it doesn’t explicitly receive the information of the lowest bandwidth link to the destination, the advertised metric itself has that information indirectly included in it. Does that make sense?

I hope this has been helpful!

Laz

24

Hi, I cant seem to make your equation work on a 10GB interface. The result is wrong by a factor of 10:

The interface:

R5#sh ip eigrp topology 155.1.5.0/24
EIGRP-IPv4 VR(CCIE) Topology Entry for AS(1)/ID(150.1.5.5) for 155.1.5.0/24
State is Passive, Query origin flag is 1, 1 Successor(s), FD is 720896
Descriptor Blocks:
0.0.0.0 (GigabitEthernet0/1.5), from Connected, Send flag is 0x0
Composite metric is (720896/0), route is Internal
Vector metric:
Minimum bandwidth is 10000000 Kbit
Total delay is 10000000 picoseconds
Reliability is 255/255
Load is 1/255
Minimum MTU is 1500
Hop count is 0
Originating router is 150.1.5.5

Minimum Throughput = (10^7 * 65536)/Bw)

Total Latency = (10^7 * 65536/10) / Bandwidth

Where Bandwidth is kbps.

Substitute bandwidth into formula:

Minimum Throughput = (10^7 * 65536)/10^7) = 65536
Total Latency = (10^7 * 65536/10) / 10^7 = 6553.6

EIGRP Composite Cost Metric = (K1 * Minimum Throughput) + (K3 * Total Latency)

EIGRP Composite Cost Metric = 65536 + 6553.6 = 72,089.6

Which is 10x smaller that the composite metric calculated by EIGRP.

Am I missing something?

Thanks.

Sam

FYI… I have been experimenting and it seems that the metric calculation is the same regardless of the interface speed being above or below 1GB. I got from formulae from EIGRP rfc7868, section 5.6.3.1:

Minimum Throughput = (10^7 * 65536)/Bw
Total Latency = ((Total delay in Picoseconds)/10^6) *65536

For the above interface:

Minimum Throughput = (10^7 * 65536)/10^7 = 65536
Total Latency = (10^7/10^6) *65536 = 655360

EIGRP Composite Cost Metric = 65536 + 655360 = 720896

Which is correct. I tried changing the BW to other values above 1GB and they also worked.

Aside from the above, I have a second question.

In the notes it says wide metrics supports a maximum interface speed of 4.2 terrabits. But the formula:

Minimum Throughput = (10^7 * 65536)/Bw)

indicates that the Bw can be up to 65536 * 10^7, which is 655.36 terrabits.

Or am I misunderstanding?

Thanks again,

Sam.