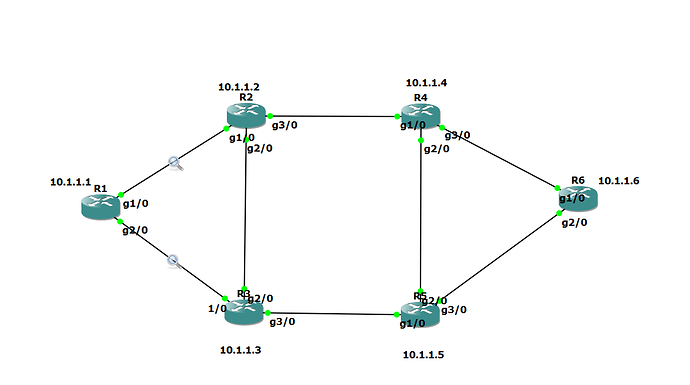
Hi ,
I want load balance my icmp traffic over ospf on attached topology , so that number of icmp req/res should be shared equaly on GigabitEthernet1/0 and GigabitEthernet2/0 . i understand currently all icmp traffic(50 req and 50 res packets) getting forwarded/received through the link R1-R2 as ospf taking lowest router id of 10.1.1.2(R2) compared 10.1.1.3(R3) . How to achieve loadbalace the traffic so that i can get 50 Req + Res on the link R1-R2 and similarly 50 Req + Res on R1-R3 ?
Sending traffic
R1#ping 200.200.200.200 source loopback 0 repeat 50
Type escape sequence to abort.
Sending 50, 100-byte ICMP Echos to 200.200.200.200, timeout is 2 seconds:
Packet sent with a source address of 100.100.100.100
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Success rate is 100 percent (50/50), round-trip min/avg/max = 48/63/80 ms
-
i have tried with maximum-paths 2 on R1 , below is my observations :
50 icmp reply packets on the link from R1-R2 . And 50 ICMP Request on the link R1-R3 (shown as no response found on wireshark capture)
-
i have deleted maximum-paths 2 config and tried with command traffic-share min across-interfaces command → 50 icmp Req and 50 responses through the link R1-R2 . (Same beha)
-
I configured R1 and R6 maximum-paths 2, behaviour is the same as case 1 as above.
Below is the common config for R2,R3,R4 and R5 :
router ospf 100
router-id 10.1.1.2
log-adjacency-changes
network 0.0.0.0 255.255.255.255 area 0
!
On R1 : Extra interface is interface loopback 0 --100.100.100.100
R1#sho ip ospf neighbor
Neighbor ID Pri State Dead Time Address Interface
10.1.1.3 1 FULL/DR 00:00:33 192.168.13.3 GigabitEthernet2/0
10.1.1.2 1 FULL/DR 00:00:33 192.168.12.2 GigabitEthernet1/0
R1#sho ip route 200.200.200.200
Routing entry for 200.200.200.200/32
Known via "ospf 100", distance 110, metric 4, type intra area
Last update from 192.168.13.3 on GigabitEthernet2/0, 00:13:23 ago
Routing Descriptor Blocks:
192.168.13.3, from 10.1.1.6, 00:13:23 ago, via GigabitEthernet2/0
Route metric is 4, traffic share count is 1
* 192.168.12.2, from 10.1.1.6, 00:13:23 ago, via GigabitEthernet1/0
Route metric is 4, traffic share count is 1
On R6 : Extra interface is interface loopback 0 --200.200.200.200
R6#sho ip ospf nei
Neighbor ID Pri State Dead Time Address Interface
10.1.1.5 1 FULL/DR 00:00:36 192.168.56.5 GigabitEthernet2/0
10.1.1.4 1 FULL/DR 00:00:31 192.168.46.4 GigabitEthernet1/0
R6#sho ip route 100.100.100.100
Routing entry for 100.100.100.100/32
Known via "ospf 100", distance 110, metric 4, type intra area
Last update from 192.168.56.5 on GigabitEthernet2/0, 00:19:52 ago
Routing Descriptor Blocks:
192.168.56.5, from 10.1.1.1, 00:19:52 ago, via GigabitEthernet2/0
Route metric is 4, traffic share count is 1
* 192.168.46.4, from 10.1.1.1, 00:19:52 ago, via GigabitEthernet1/0
Route metric is 4, traffic share count is 1