This topic is to discuss the following lesson:
Wonderful explanation. thanks
I finally found my ‘ah ha!’ moment with subnetting. Thank you so much!
Thank you for this, first time someone described subnetting in a way that makes sense. I also had that aha moment with this lesson.
Pretty minor, but just to point out on your class B and A examples subnet 2 has network address twice instead of broadcast. Just a heads up, thanks for the explanation.
Thanks for letting me know, just fixed them!
great information, i have been in a class room setting for a bit and never had it explained this way
Hi Rene
When creating this blocks, do they have to be of equal size?
For example, you have an address of 10.10.10.0/23, and I am working to create a network/mask for the below requirements
I. 24 hosts
II. 111 hosts
III. 47 hosts
IV. 200 hosts
I came up with this , can you let me know if this is correct
I. 10.10.10.0/27
II. 10.10.10.128/25
III. 10.10.10.64/26
IV. 10.10.11.0/24
If I did this way, is this correct?
I. 10.10.10.192/27
II. 10.10.11.64/25
III. 10.10.11.0/26
IV. 10.10.10.0/24
Thanks
Palani
Palani,
Short answer: Everything you have is correct. For any given subnet mask, the block size is always the same.
People do subnetting many different ways. I haven’t heard of others doing it my way, but it works for me. I thought I might share with you how I can do subnetting very fast in my head–no calculators or even pencil and paper required.
I use the formula 2^X >= Y, which reads as 2 to the Xth power is greater than or equal to Y. Y is the number of hosts (or subnets) you are trying to figure out, and X is the variable you are trying to solve for. Let’s walk through one of your examples: 47 hosts. In this case we know that Y = 47. So now we have to figure out what power of 2 is as close to 47 as possible, but cannot be less. Two to the fifth power is 32, so that’s too small. How about 6? Two to the sixth power is 64–so that’s our answer: X = 6.
So what does X do for you? A lot! Once you solve for X, you can easily figure out two things:
-
The network block size (the range of each subnet): This is simply 2^X, which in our case is 64. This means that your subnet ranges would be..
0 - 63
64 - 127
128 - 191
192 - 255
Notice how on the left column above, I just increase the number by the block size? Easy! -
The subnet mask. You will have to know which octet you are trying to figure out (in this case it is the last octet). To figure out the mask, simply subtract 2^X from 256–so in this case it would be: 256 - (2^6) = 256 - 64 = 192. Now you know the subnet mask will be 255.255.255.192. Easy!
Both Rene and Andrew are amazing. I have been stuck on this for a couple of days and all I can say is THANK YOU!! The 2^x>=Y method and the 256 - block size just about cleared all my questions. Being a full-time worker, college student, and Dad is a lot on my plate and sometimes my brain is too tired to grasp things from the textbooks and lectures. I looked at this site today and viola, I am confident now.
Jim D.
It would help if you included the subnet mask or prefix in your examples.
Hi Jeremy,
In this example we do show the subnet mask for each “block”? ![]()
Rene
Hi gyus,
I’ve done the exercises and I am most certain that they are correct, but could you leave us a link or an appendix with the solutions for confirmation purposes?
Regards,
Gerson
Hi Gerson,
A subnet calculator might be even more useful. You can use this to verify anything you calculated.
For example:
Rene
Hi Andrew,
If i require just 2 hosts for P2P, i am having trouble using your formula. Since 2^X >= Y, where Y is 2, which makes X = 1. Now with X=1, make 2^1=2. The Subnet ranges would be:
0-1
2-3
and so on.
Which I believe is not correct, since for 192.168.1.0/30 subnet, the host would be 192.168.0.1 - 192.168.0.2. Please clarify?
Use the formula (2^X) - 2 >= Y
Guys, I need help. Every time I try getting into different topics, be it NAT, Routing Policy, etc - I always get back to Subnetting. I finally realized there’s no way to progress without mastering this subject. I google everywhere, but I need your help and hopefully I’ll finally figure this out. Please, show me how would you answer this question;
Write a standard ACL that will cover the host range from 192.168.100.128 through 192.168.100.131.
Let’s not worry about the ACL part, but how would you go about writing an IP address with a subnet (wildcard) mask that would cover the need for 3 usable hosts?
You’d really help me out a lot.
Thank you in advance.
Hi Maros,
Once you understand the fundamentals of subnetting, a quick way to solve a question like this is to visualize it and think in “blocks”:
And take a look at VLSM:
We want an access-list that matches four addresses, it starts with 192.168.100.128:
- 192.168.100.128
- 192.168.100.129
- 192.168.100.130
- 192.168.100.131
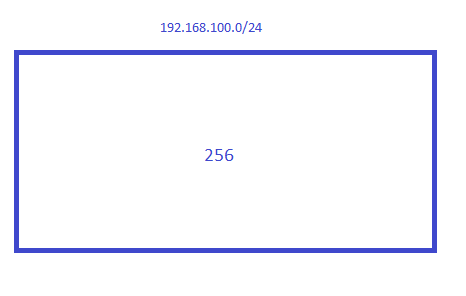
The first thing we need to figure out is what these addresses are. Is it an exact subnet? In this case, it might be easy to see but if someone asks you to block “192.168.100.44/29”, you’ll need to figure this out. A quick way to find out is to visualize the 192.168.100.0/24 subnet as a “block” of 256 addresses:
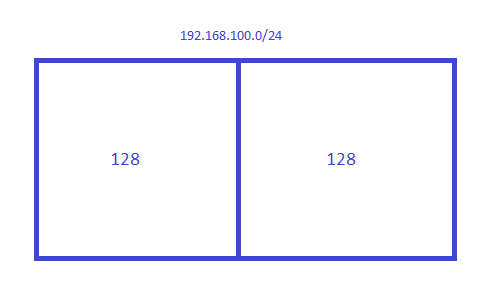
If I cut it in half, I get two blocks:
You get two blocks of 128 so there are two subnets:
- Subnet 1: 192.168.100.0 - 192.168.100.127
- Subnet 2: 192.168.100.128 - 192.168.100.255
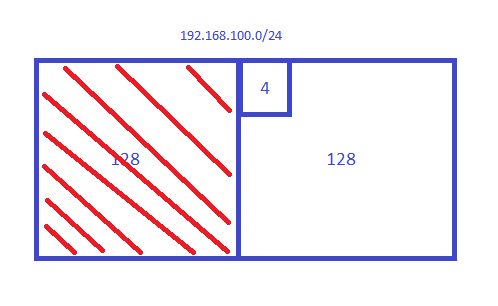
This quickly tells me that 192.168.100.128 is a network address and since you specify four addresses, (a block of four), we know it’s an exact subnet that you try to match.
The range you want to match is not in the first block so we can forget about it. It is on the second block though:
So what’s the subnet mask for your subnet? A quick way to figure that out is to take the number 256 minus the block size:
256 - 4 = 252
We are working in the fourth octet so your subnet mask is 255.255.255.252
Now since we need a wildcard instead of a subnet mask, we have to convert it. In binary, the subnet mask looks like this:
11111111 11111111 11111111 11111100
A wildcard is an “inverted” subnet mask so we just flip the bits:
00000000 00000000 00000000 00000011
Which gives us a wildcard of 0.0.0.3
A quicker method is just to take the block size minus 1. Our subnet is a block of 4, so the wildcard becomes 3.
- If you have a subnet that has 8 addresses, the wildcard is 7.
- If you have a subnet that has 16 addresses, the wildcard is 15.
- Etc
These “tricks” make it easier to quickly answer questions like this but make sure you understand the fundamentals, otherwise, you have no idea why we use these tricks. If not, you might want to go over the binary examples first:
Hope this helps!
Rene
Hi Rene,
Thanks for the great work. You are really making the topics easy to understand. One observation I want you to clarify is what you said about every bit borrowed doubles you network. It is true for the 1st and the 2nd bit but does not appear to be true for 3 bits and up. Can you confirm?
Hello Charles,
Glad to hear you like it!
This logic applies to all bits. Let’s look at an example for subnet 192.168.1.0/24. We need to look at the fourth octet where the host bits are. In binary it looks like this:
00000000
Right now we have 8 host bits and 1 subnet. Let’s borrow one host bit so we can create more subnets.
10000000
Now we have 2 subnets and 7 host bits. Let’s borrow one more:
11000000
Now we have 4 subnets and 6 host bits. Let’s borrow one more:
11100000
Now we have 8 subnets and 5 host bits. Let’s borrow one more:
11110000
Now we have 16 subnets and 5 host bits. You can continue like this.
Does this make sense?
Rene