Subnetting in Decimal (Fast Way)

Lessons Discussion
18

Hi Maros,

Once you understand the fundamentals of subnetting, a quick way to solve a question like this is to visualize it and think in “blocks”:

And take a look at VLSM:

We want an access-list that matches four addresses, it starts with 192.168.100.128:

  • 192.168.100.128
  • 192.168.100.129
  • 192.168.100.130
  • 192.168.100.131

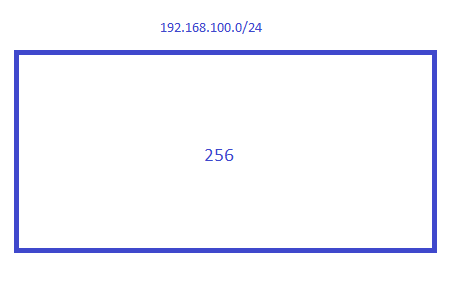
The first thing we need to figure out is what these addresses are. Is it an exact subnet? In this case, it might be easy to see but if someone asks you to block “192.168.100.44/29”, you’ll need to figure this out. A quick way to find out is to visualize the 192.168.100.0/24 subnet as a “block” of 256 addresses:
block-256
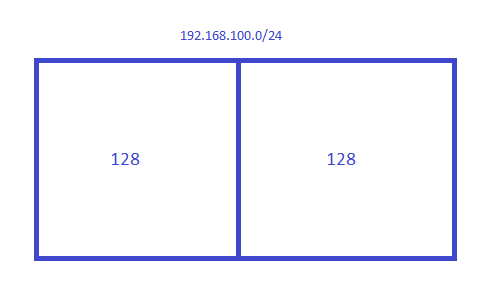
If I cut it in half, I get two blocks:
blocks-128
You get two blocks of 128 so there are two subnets:

  • Subnet 1: 192.168.100.0 - 192.168.100.127
  • Subnet 2: 192.168.100.128 - 192.168.100.255

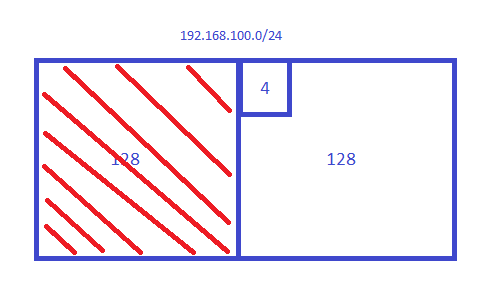
This quickly tells me that 192.168.100.128 is a network address and since you specify four addresses, (a block of four), we know it’s an exact subnet that you try to match.

The range you want to match is not in the first block so we can forget about it. It is on the second block though:
blocks-4
So what’s the subnet mask for your subnet? A quick way to figure that out is to take the number 256 minus the block size:

256 - 4 = 252

We are working in the fourth octet so your subnet mask is 255.255.255.252

Now since we need a wildcard instead of a subnet mask, we have to convert it. In binary, the subnet mask looks like this:

11111111 11111111 11111111 11111100

A wildcard is an “inverted” subnet mask so we just flip the bits:

00000000 00000000 00000000 00000011

Which gives us a wildcard of 0.0.0.3

A quicker method is just to take the block size minus 1. Our subnet is a block of 4, so the wildcard becomes 3.

  • If you have a subnet that has 8 addresses, the wildcard is 7.
  • If you have a subnet that has 16 addresses, the wildcard is 15.
  • Etc

These “tricks” make it easier to quickly answer questions like this but make sure you understand the fundamentals, otherwise, you have no idea why we use these tricks. If not, you might want to go over the binary examples first:

Hope this helps!

Rene

1 Like