Introduction to Spanning-Tree

Lessons Discussion
162

Hello Narad.

Most of the answers to these questions can be found in the lessons themselves. For now I’ll try to briefly answer them here.

Q1: This is the port priority and port number. A combination used to determine which port will be blocked in the event there are two or more links between two switches. The Prio is the priority set by default to 128, and it is 8 bits and the Nbr is a number that is assigned to this port, and this is another 8 bits. Together they represent the priority of the port. More about this at the end of the Spanning Tree Cost Calculation lesson.
Q2: Take a look at this post.
Q3 and Q4: Source mac address is the mac of the interface that sends out the BPDU ( if the interface has a mac address, if not, it will use one mac address reserved for the system use for protocol packets like BPDU in STP). The destination address is the multicast address reserved for STP 01-80-c2-00-00-00.
Q5: MACs for SVIs are assigned depending upon the platform. Some use the same MAC address for all, while others will use one from a pool of MAC addresses made available to the device. These are preconfigured or hardcoded in the device from the factory.
Q6: By default, BPDUs can be received on blocked ports.
Q7: This is described in detail in the Introduction to Spanning Tree lesson.
Q8: BPDUs are sent to directly connected neighbors. The neighbors will then relay the BPDUs down the STP tree until all switches receive the BPDUs.
Q9: I’m not sure I understand the question.
Q10: Convergence is described in the Introduction to Spanning Tree lesson.
Q11: Reconvergence will take place in the same way for both cases.
Q12: I’m not sure I understand the question.

I hope this has been helpful!

Laz

163

Can we use STP as difference mode and BPUD can update with together ?

164

Hello Suphakorn

It is possible to run different STP modes and have them work together, but this should be done with care. For example, RSTP is backwards compatible with standard STP. Similarly, MSTP is compatible with RSTP, and even PVST and RSTP can be made to function together. However, it is always a good idea to try to keep the same STP mode on all of your network in order to avoid any L2 loops that may occur due to an incorrect configuration or a difficulty in the interoperation of two different STP versions.

I hope this has been helpful!

Laz

166

Hi guys from NetworkLessons.com,

First, I would like to congratulate you for the lessons in the website. They are very good and didactic.

However, in this first lesson (Introduction to Spanning-Tree), you guys just introduce Spanning-Tree as a protocol to eliminate loops from a topology, and shared only 2 very simple examples: 2 switches with a redundant link, and a triangle (3 switches in full mesh).

Although explanation is correct, I’m afraid that they aren’t enough and people don’t understand how:

  • SPT will work for bigger and complex topologies
  • Why a root election is really necessary and important
  • Understand that links will not be utilized - no traffic (besides BPDU) will be send (so this is a disadvantage of switched layer-2 networks)

In my opinion, you should add a more complex example (a bigger topology graph). Goal should not be to explain step-by-step how the STP would run to prune links (because it would be hard for newcomers to understand). Goals show be just to explain what a spanning-tree really is, and by doing this, clarify the concepts.

Let me explain what I mean:

  1. Explain what a tree is
  2. Explain what a spanning tree is
  3. Explain what STP actually does: remove links from a non-tree topology (with loops) until transform it into a spanning-tree (tree created from the original topology, so it doesn’t contain any loops). And because STP goal is to create a tree, it must contain a root.

Of course, if you go into the mathematical definitions of graph, tree and spanning tree, it will become complex for newcomers. But for simplicity, I think you can just introduce a tree as a topology where we start with a root node, and each node can have child nodes. A child node can only have a single parent, but may have other child nodes.

The examples that may clarify very well all concepts was already created by you. You have an excellent example at lesson Spanning-Tree Cost Calculation.

I think you can explain concepts using the following logic.

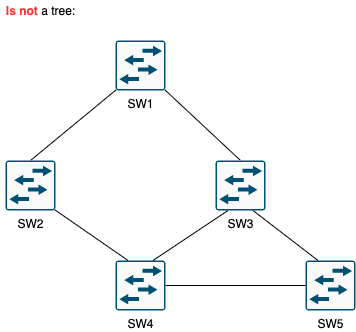
  1. Example 1 - Not a tree, because SW 4 and SW 5 has two parents.

example-1

Note that, connected non-tree topologies contain loops.

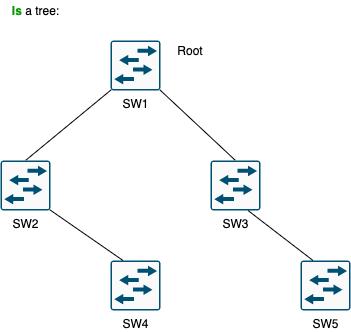
  1. Example 2 - A tree, because is connected and every SW or is the root or only have a single parent

example-2.png
image

Note that, tree topologies does not contain loops.

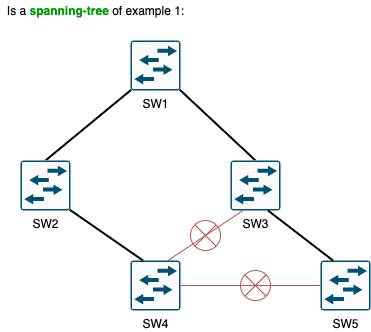
  1. Example 3 - Spanning tree, because is a tree build from the original topology via removing links until all loops are removed

It’s possible to eliminate links into a non-tree with loop topology until we can transform it into a tree (without loops). When we do this, we call the new tree a spanning-tree. This is exactly what STP does: it eliminates links until all loops are eliminated and we end up with a tree.

stp-example-Page-3.png
image

In order to create a spanning-tree from a topology with loops (non-tree), STP starts choosing the root for the tree.

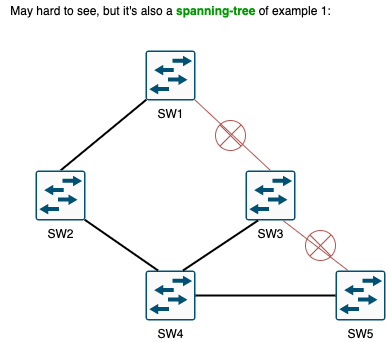
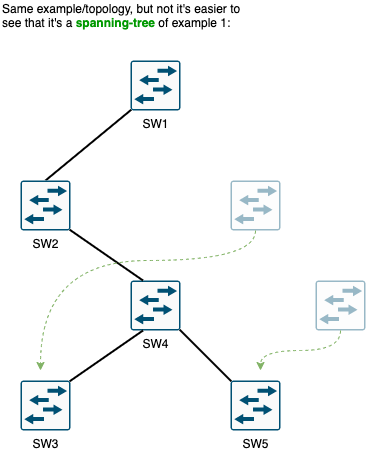
  1. Example 4 - Also a spanning tree

example-4.png
image

To make easier to see that this is a spanning-tree, let’s re-draw the same topology, but moving SW3 and SW5:

example-5

  1. To finish, you may want to reintroduce the first 2 examples and explaining why they are not trees

Example SW1 <-> [2 links] SW2 is not a tree because there are 2 connections between the nodes, and in a tree, the root node or a parent node can only have a single connection to its child

Example SW1 <-> SW2 <-> SW3 <-> SW1 is not a tree because, if we consider SW1 as a root, and SW2 as a child from SW1, then SW3 will have 2 parents.

You may also want to join everything together into a new and isolated lesson.

----

Final note: At least to me, it is much much much easier to understand the STP protocol when we know what is a tree, and what is a spanning-tree. Otherwise, people may understand STP in a topology with 3 SWs, but maybe they will not understand complex topologies.

1 Like
167

Hello Rarylson

Thank you so much for your contribution! This is one of the things that makes this site so great, participants like you that add to the value of the forum.

It is true that understanding the underlying theory of a tree and the significance of that tree for STP is important to further understand how STP works, especially in more complex topologies. The material you included in your post is helpful in this.

I will inform Rene about your thoughts as well.

Thanks again for your contribution!

Laz

168

When you implement rate limit on interfaces… does it influence the cost of the link? regardless of interface type (FasE, GigE etc.).

Duplex settings… does it matter when implementing STP/RSTP?

169

@ReneMolenaar Okay, I’m confident that I could be incorrect, I am wondering if the behavior happens is flooding and not a broadcast, as the ethernet frame sent by host 1 on sw1 in the diagram sends a unicast frame to h2 on sw2 on the topology that is explained here?

172

Hello Mylene

That’s a very good question! The STP cost of any interface is only based on the type of interface (FastEthernet, GigabitEthernet, 10GigabitEthernet etc…). The only way to change the cost is to use the spanning-tree cost command similar to the following example:

SW3# conf t
SW3(config)# interface gi1/0/1
SW3(config-if)# spanning-tree cost 1

Another way to change the cost is to change the speed setting on the interface. For example, if you apply speed 100 to a GigabitEthernet port, it will change the cost to that of a FastEthernet port. For example:

SW3#conf t
Enter configuration commands, one per line.  End with CNTL/Z.
SW3(config)#inter gig 0/0
SW3(config-if)#speed 100
SW3(config-if)#exit
SW3(config)#exit
SW3#show spanning-tree 

VLAN0001
  Spanning tree enabled protocol ieee
  Root ID    Priority    32769
             Address     5254.000c.f48d
             Cost        4
             Port        2 (GigabitEthernet0/1)
             Hello Time   2 sec  Max Age 20 sec  Forward Delay 15 sec

  Bridge ID  Priority    32769  (priority 32768 sys-id-ext 1)
             Address     5254.0018.c0d4
             Hello Time   2 sec  Max Age 20 sec  Forward Delay 15 sec
             Aging Time  300 sec

Interface           Role Sts Cost      Prio.Nbr Type
------------------- ---- --- --------- -------- --------------------------------
Gi0/0               Desg FWD 19        128.1    P2p 
Gi0/1               Root FWD 4         128.2    P2p 
Gi0/2               Altn BLK 4         128.3    P2p 


SW3#

Above you can see that the Gi0/0 interface now has a cost of 19, which corresponds to the cost of a FastEthernet port.

Also keep in mind that the actual cost value will depend upon the method of cost calculation, that is, using the original STP cost or using what is known as the long mode.
More info on this can be found at the NetworkLessons Note on STP cost calculation methods.

Finally, the duplex settings do not affect how STP functions, as long as the duplex settings are correct on both ends of the link. In the event that there is a duplex mismatch, STP can break down, as shown in this Cisco documentation:

I hope this has been helpful!

Laz

173

Hello Vivek

You are correct that the frame being sent from H1 to H2 is a unicast frame with a specific MAC address (that of H2) in the destination field of the Ethernet header. However, Rene here is talking about the ARP request, which is indeed a broadcast frame. ARP is used to learn the desired MAC destination address (in this case, that of H2) from the known IP address of H2. For more info on ARP, take a look at this lesson:

You do bring up a good point, however, that broadcast and flooding are two different things, but under certain circumstances, they behave the same. For example, if a switch has no entries in its MAC address table, a unicast frame received by the switch will be flooded out of every switch port except the ingress port. Similarly, a broadcast frame will be treated the same way. However, once the MAC address table is populated, all subsequent unicast frames are sent out of the interface corresponding to that MAC address in the MAC address table.

More details about this can be found here:

I hope this has been helpful!

Laz

174

What does a switch do with BPDUs when the spanning tree is disabled?.

175

Hello Arun

When STP is disabled on a particular VLAN, and BPDUs received on that VLAN are forwarded just like any other multicast traffic. You can find more detailed info at these NetworkLessons notes:

I hope this has been helpful!

Laz

176

in the example you said the mac is the tie breaker, you said the mac address is lower… what exactly do you mean? AAA,BBB,CCC what determines if a mac address is higher or lower?

177

Hello Patrick

This is an excellent question that we don’t often address directly. Remember that MAC addresses are essentially numbers. By convention, MAC addresses are written in Hexidecimal. Computers and network devices actually read MAC addresses as binary. We can even write out a MAC address in decimal format, although we never do that because it has no use to us.

So a MAC address of 00:00:00:00:00:01, if simply viewed as a number, is smaller than 00:00:00:00:00:02. Similarly AB:00:00:00:00:00 is smaller than AC:00:00:00:00:00. Some more examples:

  • AB:CD:EF:12:34:56 is larger than AB:CD:EF:12:34:11
  • 00:00:00:55:55:55 is larger than 00:00:00:44:55:55
  • FF:FF:FF:FF:FF:FF is larger than 00:00:00:00:00:00

IPv4 addresses are also often used as tiebreakers, where the higher or lower IP address “wins”. This is more readily understandable because IPv4 uses the dotted decimal format, which we as humans are more familiar with.

I hope this has been helpful!

Laz

178

That makes total sense

Thank you!

1 Like
179

Question: BPDU Frame

How dose the switch determines a frame is a BPDU frame?

180

Hello Patrick

Take a look at this NetworkLessons note that describes the contents of a BPDU. From this, you can see that a BPDU has a specific structure and includes a protocol identifier that indicates what type of STP is being used, and also includes an identifier that states what type of BPDU is being sent.

Beyond the structure of the BPDU itself, there are lower layer protocols that also indicate to a switch receiving a frame, that it is a BPDU being sent. Take a look at this cloudshark capture of a BPDU frame being sent:

image
image706×481 17.3 KB

(this was taken from this cloudshark capture)

The BPDU frame information shown in the note above only deals with the layer of the packet titled Spanning Tree Protocol near the bottom of the capture.

Note that this BPDU is encapsulated within a Logical Link Control (LLC) layer PDU, which contains the information in the Destination Service Access Point (DSAP) field as a Spanning Tree BPDU, with a code of 0x42. This tells the switch that the encapsulated information is an STP BPDU.

But even that LLC layer is encapsulated within an IEEE 802.3 Ethernet frame, which in turn uses a destination MAC address of 01:80:c2:00:00:00. This is a well-known destination MAC address defined by IEEE 802.3D as the Spanning Tree for Bridges destination address.

All of the above information tells the switch that this is a BPDU, and it is interpreted as such.

I hope this has been helpful!

Laz

181

Thank you

I realize now that I need to learn more about 802.3; most of my training has been focused on ethernet 2.

Is there any recommended reading for the 802.3 frame format? I feel like gaining a better understanding here would do me some good.

Thanks.

182

Hello Patrick

Indeed, 802.3 Ethernet is a somewhat confusing concept when you know that both 802.3 and Ethernet II can operate seamlessly over the same infrastructure. I don’t have something specific to suggest for training material, but you can take a look at this post for some more info:

I will also create a NetworkLessons Note on this topic soon with some additional links, so you can also look out for that.

I hope this has been helpful!

Laz

183

Much Appreciated. That would be very helpful.

1 Like
184

Hello Patrick.

Here’s the NetworkLessons note on the topic of Ethernet frame types that I promised you.

Have a great day!

Laz